輸送現象の理論
輸送現象における量子効果および臨界現象
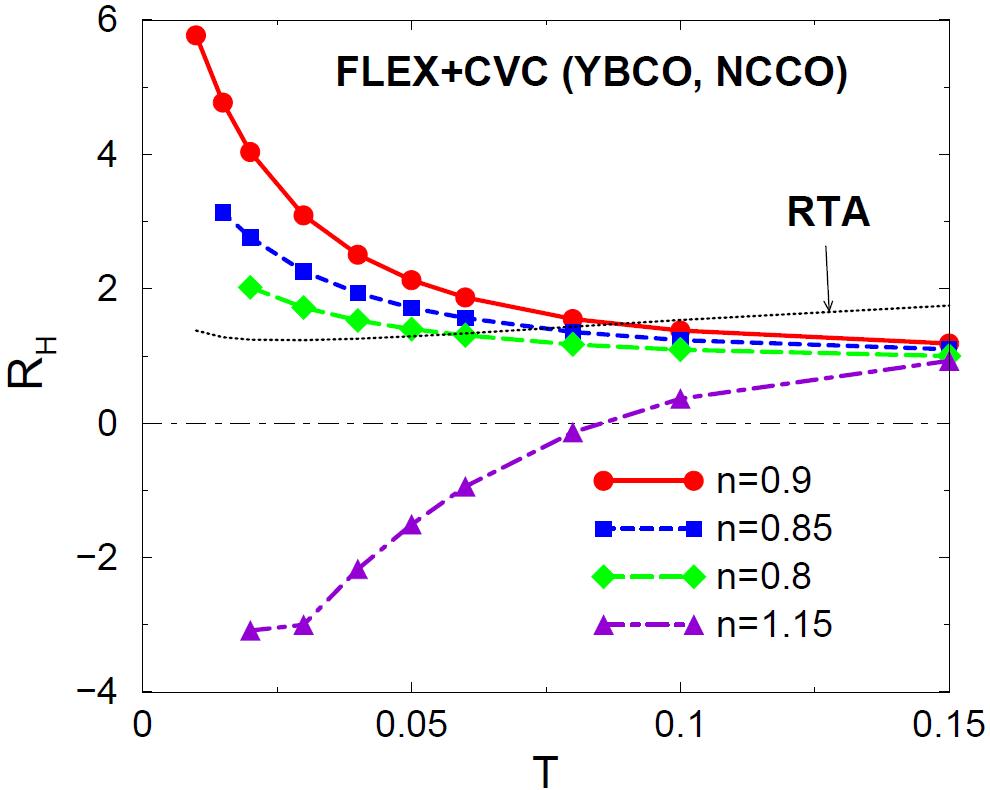
バーテックス補正を取り入れて計算されたホール
係数の温度依存性。T=0.1は約400Kに相当する。
電子ドープの場合(n=1.10)、ホール係数は低温
で負になる。
1986年に発見された銅酸化物高温超伝導体は、超伝導転移温度Tcが160Kに達する。その超伝導発現機構の解明の鍵として、異常金属相と呼ばれるTc以上の領域における物理量の異常な振舞い(非フェルミ液体的挙動)が注目を集めてきた。例えばホール係数は広い温度領域でキュリー・ワイス的な振舞いを示し、特に、電子ドープ系のフェルミ面は「ホール的」であるにもかかわらず、負の値を示す。これらの振舞いは単純なボルツマン近似(緩和時間近似)では全く説明ができないため、しばしばフェルミ液体的描像の破綻の証拠とみなされてきた。
そこで我々は、カレントに対する「バーテックス補正」を正しく解析する手法を開発した[1-4]。その結果、ホール係数や磁気抵抗、熱起電力、ネルンスト係数等の異常な振舞いが、「反強磁性揺らぎの強いフェルミ液体」として自然に統一的に理解できることが明らかになった。この理論は反強磁性相近傍の金属一般で普遍的に成り立つ「量子臨界現象」を記述する理論であり、重い電子系 CeMIn5(M=Co, Rh, Ir) や、有機超伝導体κ-(BEDT-TTF)の輸送現象の異常も説明可能である。さらに、鉄系超伝導体の電子ネマティック秩序状態における異方的輸送現象を解明した[5]。
更に、スピンホール効果や異常ホール効果などの量子輸送現象における軌道自由度の重要性を解明した。我々はいち早く4d,5d遷移金属のスピンホール効果を網羅的に解析し、巨大な内因性ホール効果が普遍的に出現することを見出した[4,6-9]。我々の理論的予言は、大谷研による精密測定により立証された。またパイロクロア化合物Nd2Mo2O7におけるトポロジカルホール効果を、軌道自由度を考慮することで解明した[10,11]。
[1] H. Kontani, K. Kanki, and K. Ueda, Phys. Rev. B 59, 14723 (1999).
[2] H. Kontani, Phys. Rev. Lett 89, 237003 (2002).
[3] H. Kontani, Rep. Prog. Phys. 71, 026501 (2008).
[4] H. Kontani, "Transport Phenomena in Strongly Correlated Fermi Liquids"
(Springer Berlin Heidelberg, Berlin, Heidelberg, 2013).
[5] S. Onari and H. Kontani, Phys. Rev. B 96, 094527 (2017).
[6] H. Kontani et al., Phys. Rev. Lett. 100, 096601 (2008).
[7] H. Kontani et al., Phys. Rev. Lett. 102, 016601 (2009).
[8] H. Kontani, J. Goryo, and D. S. Hirashima, Phys. Rev. Lett. 102, 086602 (2009).
[9] M. Morita et al., Phys. Rev. B 83, 174405 (2011).
[10] T Tomizawa, and H. Kontani, Phys. Rev. B 80, 100401(R) (2009).
[11] T. Tomizawa and H. Kontani, Phys. Rev. B 82, 104412 (2010).