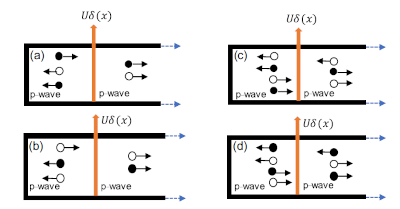
We study a Kitaev chain model, which is the simplest model of topological superconductors hosting Majorana fermion, appearing as a zero-energy state at the edge. We analytically calculate the Green's function of the semi-infinite Kitaev chain with a delta-function-type impurity potential within the quasiclassical regime to obtain the spatial dependence of the induced odd-frequency pairing. It is found that if the position of the impurity is not far from the edge, the spatial profile of the local density of states (LDOS) and the odd-frequency spin-triplet s-wave pair amplitude is tunable as a function of the strength of the impurity potential. Moreover, the zero-energy LDOS and low-frequency odd-frequency pair amplitude are found to have the same spatial dependence. The spatial profile of the zero-energy LDOS is analyzed based on the wave function of Majorana fermions.

(Click figure for a larger image.)