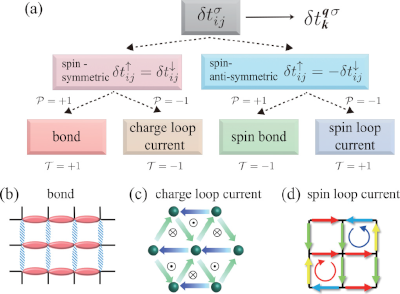
Rigorous formalism for unconventional symmetry breaking in Fermi liquid theory and its application to nematicity in FeSe
R. Tazai, S. Matsubara, Y. Yamakawa, S. Onari, and H. Kontani, ,
Phys. Rev. B 107, 035137 (2023).
Published 23 January 2023
Unconventional symmetry breaking due to nonlocal order parameters has attracted considerable attention in many strongly correlated metals. Famous examples are the nematic order in Fe-based superconductors (SCs) and the star-of-David charge density order in kagome metals. Such exotic symmetry breaking in metals is a central issue of modern condensed matter physics, while its theoretical foundation is still unclear in comparison with the well-established theory of superconductivity. To overcome this difficulty, here, we introduce the form factor that generalizes the nonlocal order parameter into the Luttinger-Ward (LW) Fermi liquid theory. We then construct a rigorous formalism of the density-wave equation that gives the thermodynamically stable form factor, like the SC gap equation. In addition, a rigorous expression of the Ginzburg-Landau free energy for the unconventional order is presented to calculate various thermodynamic properties. In the next stage, we apply the derived formalism to a typical Fe-based SC FeSe, by using the one-loop LW function that represents the free-energy gain due to the interference among paramagnons. The following key experiments are naturally explained: (i) Lifshitz transition (=disappearance of an electron pocket) due to the bond + orbital order below Tc; (ii) Curie-Weiss (CW) behavior of the nematic susceptibility at higher T, and the deviation from the CW behavior at lower T near the nematic quantum critical point; and (iii) scaling relation of the specific heat jump at Tc, ΔC/Tc∝Tbc with b∼3. (Note that b=0 in the Bardeen-Cooper-Schrieffer theory.) These results lead to a conclusion that the nematicity in FeSe is the bond + orbital order due to the paramagnon interference mechanism. The present theory paves the way for solving various unconventional phase transition systems.
(Click figure for a larger image.)