ReserchResearch
Unconventional Superconductivity
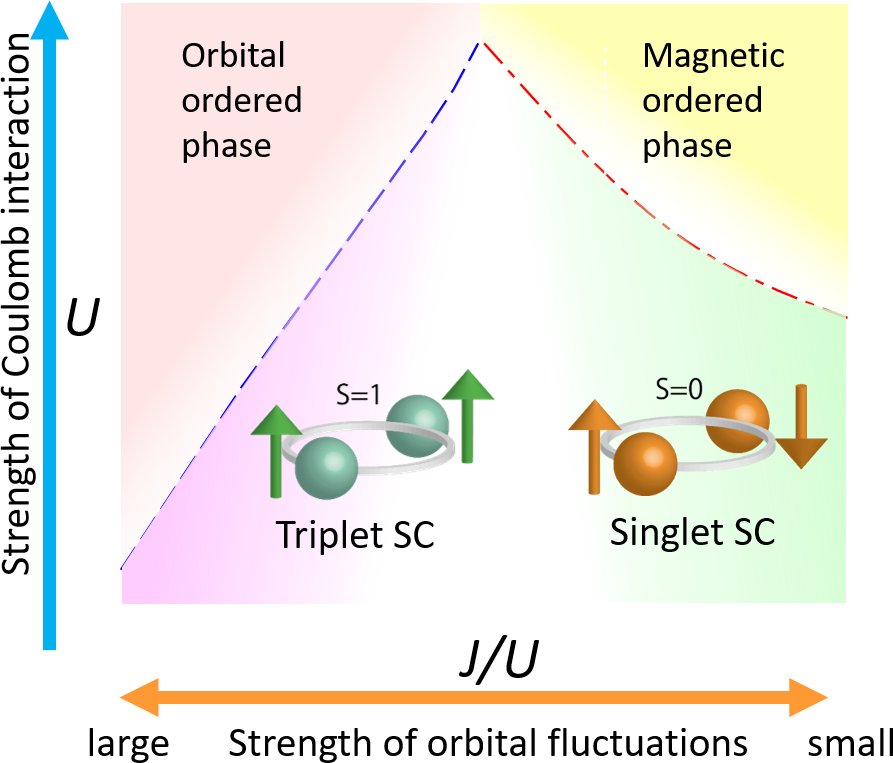
Obtained superconducting phase diagram
for two-orbital Hubbard model.
The superconductivity with zero resistivity is an interesting phase transition of electrons in metals, which occurs when electrons form pair states (Cooper pair). In conventional superconductors, the pairing glue of Cooper pairs is given by the electron-phonon interaction. In unconventional superconductors in strongly correlated electrons, in contrast, the pairing interaction is derived from the Coulomb repulsion. Rich variety of unconventional superconductivity is one of the central issues in modern physics.
In our laboratory, we perform theoretical research on high-temperature superconductivity. In cuprate high-temperature superconductors (Tc <160K), quantum spin fluctuations of electrons lead to d-wave Cooper pairs. In Fe-based superconductors (Tc = 60K to 100K), quantum fluctuation of d-orbital degrees of freedom (= orbital fluctuations) contribute to the significant pairing mechanism. In addition, when spin fluctuations and orbital fluctuations develop cooperatively, various exotic superconducting states can emerge, such as the spin-triplet (S=1 Cooper pair) superconductivity. There are many other unconventional superconductors such as heavy fermion systems, organic conductors, and Co, Ni, Cr compounds. Let us study novel superconducting states in Sc Lab!
Please see Orbital Fluctuation Mechanism in Fe-based Superconductors, Mystery in Spin Triplet Superconductivity
Strongly Correlated Electrons
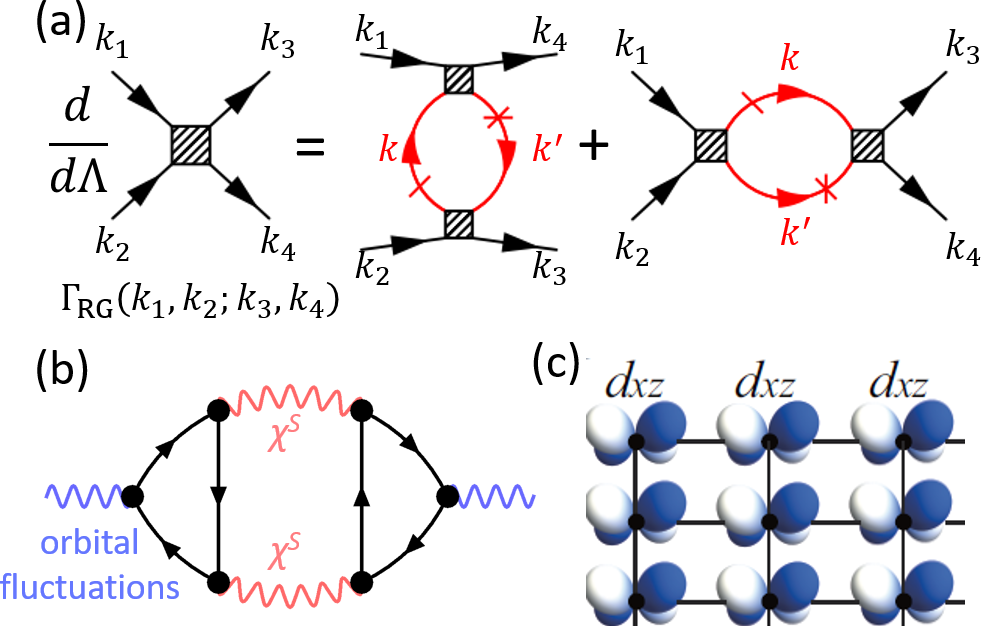
(a) Feynman diagram of nenormalization group equation.
Low-energy effective interaction is obtained by integrating
high-energy scattering processes step by step.
(b) Aslamazov-Larkin process that drives the orbital
order/fluctuations. (c) Orbital ordered state nxz≠nyz.
Strongly correlated electron systems are treasure houses of novel physical phenomena such as high-temperature superconductivity, but conventional (mean-field-level) theoretical analyses have been prevented by strong Coulomb interaction. To attack these issues, we has been actively developing new theoretical methods such as large-scale Feynman diagram calculations, and has elucidated novel physical phenomena in many strongly correlated electron systems. Recently, the renormalization group theory, which was developed by K. G. Wilson (Nobel Prize in 1982), has applied the study of strongly correlated electron systems.
The strongly correlated electron systems are also treasure houses of quantum phase transition phenomena. Recently, the "electron liquid crystal order" having a liquid crystal structure has been discovered one after another, and has become one of the central issues. Based on the latest electron correlation theory, we discovered that rich orbital orders observed in iron-based superconductors, and exotic bond orders (= charge order with d-wave symmetry) realized in cuprate superconductors. Recent research has shown that liquid crystal order appears universally in many unconventional superconductors, and their quantum fluctuations mediate exotic unconventional superconductivity. Once the mechanism of electronic liquid crystals is solved, we can naturally understand the mechanism of superconductivity.
Please see "Quantum Liquid Crystal (QLC)" in cuprate superconductors,"Grand kadowaki-Woods relation" in heavy fermion systems
Massless Dirac particles in condensed matter physics

The band structure (Dirac cone) of the
Dirac electron in α-(BEDT-TTF) 2I3.
Massless particles in vacuum travel at speed of light with kinetic energy proportional to momentum. In condensed matter, there are exotic conduction electrons which behave like massless particles, while those speed are much slower than light. Such massless (or nearly massless) particles have been discovered in graphene (Nobel Prize 2010), organic conductors, bismuth compounds, etc., and are called "Dirac electron systems". We have focused on electron correlation effects in the Dirac electron systems, because Coulomb repulsion between the Dirac electrons reaches long range in contrast to conventional metals. We have found anomalous spin fluctuation (giant Koringa ratio) and precursor phenomena of “excitonic pairing" (electron-hole pairing like the cooper pair). Those results have been confirmed by nuclear magnetic resonance measurements of Kanoda Lab. (Tokyo Tech.). In addition, an "edge state" due to topological property appears on surface of the Dirac electron system. We have found that the insulator phase of α-(BEDT-TTF)2I3 is metallized by the edge states on the domain walls. Dirac electrons also exist in the d- and f- electron systems. We have predicted an interesting spin transport phenomenon originating from Dirac electrons in iron-based superconducting KFe2As2.
Please see Dirac Electron System in Solid State Physics
Transport Phenomena
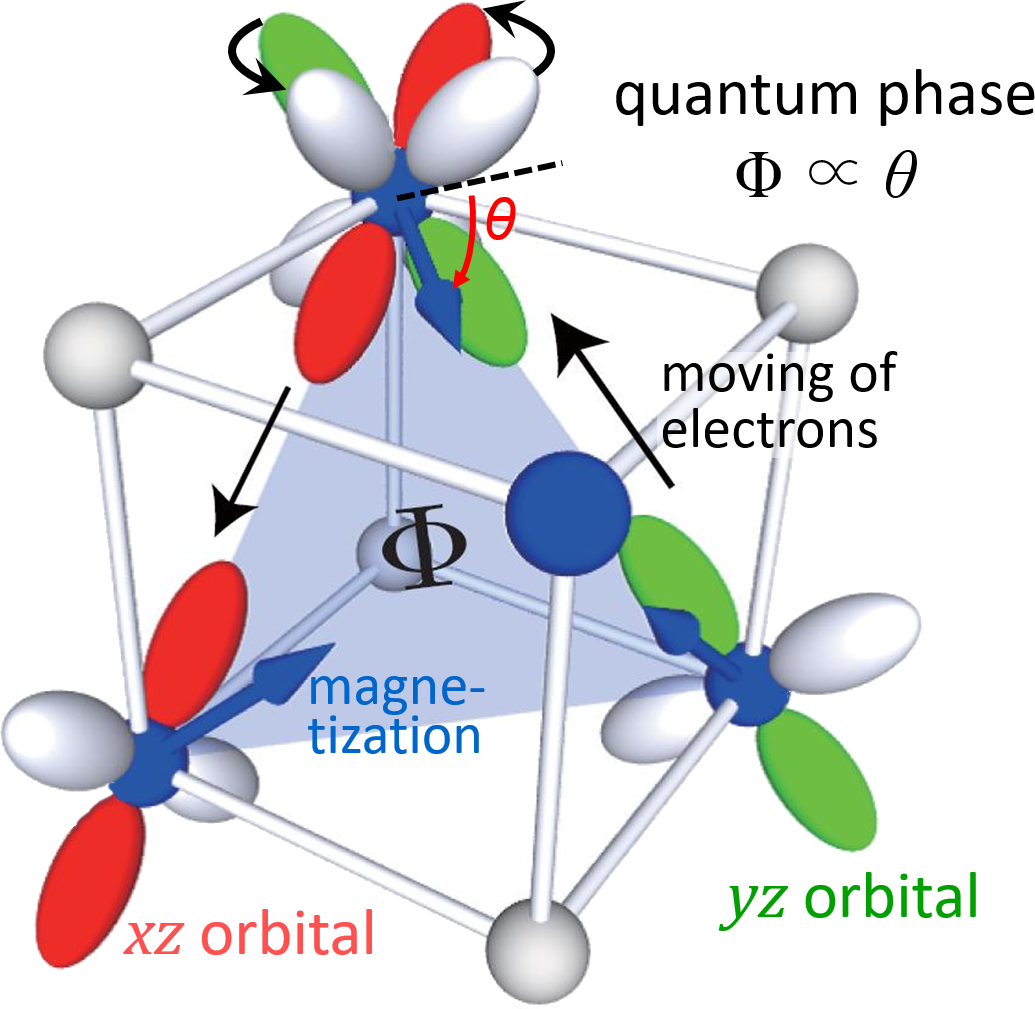
Mechanism of topological Hall effect in Nd2Mo2O7.
Hall effect originates from the Berry phase of
electrons induced by the magnetic structure.
There are a lot of novel physics in transport phenomena, in which electrons carry current and heat current. For example, “Hall effect”, where an electromotive force is generated in the direction perpendicular to the electric and magnetic fields, shows significant temperature dependence and strongly enlarged in high-Tc superconductors. The relation between the transport phenomena and mechanism of superconductivity is interesting and important. We have developed a theory of transport phenomena taking account of higher-order many-body effects (vertex correction) and found that the Hall effect is significantly enhanced by a quantum mechanics process due to the spin- and orbital-fluctuations. This study proposes that the quantum fluctuations, which enhance the Hall effect, mediate high-Tc superconductivity. As transport phenomena similar to the Hall effect, there are “anomalous Hall effect” in ferro-magnetic metals and “spin Hall effect”, where spin current appears in paramagnetic metals. We theoretically predicted spin Hall effect in 4d, 5d transition metal, which was confirmed by precise measurement in Otani Lab (ISSP). We also explained “topological anomalous Hall effect” by focusing on Berry phase induced by non-collinear spin structure in pyrochlore Nd2Mo2O7 (θ~2°) and antiferro-magnet Mn3Sn(θ=90°). “Valley Hall effect”, where the valley of electron dispersion is used as degree of freedom instead of spin, is observed in bilayer graphene by Tarucha Lab (Tokyo Univ.). We predict the valley Hall effect induced by the Berry phase due to the charge order of Dirac electrons in organic conductors.
Please see Novel quantum critical effects in transport phenomena
Recent Doctoral and Master's Theses
[Doctoral Theses]
- 大木 大悟
lectron correlation and transport phenomena in organic Dirac electron systems α-(BEDT-TTF)2I3 and α-(BEDT-TSeF)2I3 (有機ディラック電子系α-(BEDT-TTF)2I3 およびα-(BEDT-TSeF)2I3 における電子相関
2022年3月 - 松原 舜
Theory of edge induced quantum critical phenomena in strongly correlated system
(強相関電子系における表面誘起量子臨界現象の理論)
2022年3月 - 川口 功起
銅酸化物高温超伝導体における電子相関に由来する電子ネマティック秩序
2021年3月 - 田財 里奈
Theory of Multipole Fluctuation Mediated Superconductivity and Multipole Phase:Important Roles of Many Body Effects and Strong Spin-Orbit Coupling
(多極子揺らぎ誘起の超伝導及び多極子秩序相の理論研究:多体効果及びスピン軌道相互作用の重要性)
2020年3月 - 中岡 宏徳
鉄系超伝導体におけるネマティック秩序と超伝導発現機構の理論研究
2019年3月 - 松野 元樹
Efects of Coulomb interaction in the spin susceptibilityof an organic Dirac electron system-(BEDT-TTF)2I3
(有機ディラック電子系α-(BEDT-TTF)2I3のスピン感受率におけるクーロン相互作用の効果)
2018年3月 - 齋藤 哲郎
Theoretical study on superconducting gap structures and pairing mechanisms of iron based superconductors
(鉄系超伝導体における超伝導ギャップ構造及びペアリング機構の理論研究)
2015年3月 - 山下 耕平
強い斥力ポテンシャルが作用する多粒子系の気体-固体相転移に対する量子効果の研究
2014年3月 - 西根 達郎
傾斜ディラックコーンをもった2次元導体における動的誘電応答の理論
2012年3月 - 大森 有希子
TTM-TTP塩の分子内電荷秩序における多軌道効果
2011年3月 - 熊崎 秀樹
Vacancy-induced Magnetism and Spin-Polarized Current in Graphen
(グラフェン上の空孔が引き起こす磁性とスピン偏極電流)
2010年3月 - 野々山 嘉人
Theory of Charge and Spin Fluctuation-Induced Superconductivityin Quasi-two-dimensional Organic Conductor
(擬二次元有機導体におけるスピン・電荷揺らぎによる超伝導の理論)
2009年3月 - 片山 新也
Massless Dirac Particles in the Quasi-Two-Dimensional Organic Conductor
(擬二次元有機導体における質量ゼロのディラック粒子)
2008年3月 - 杉林 卓
Valence Instability in an Extended Periodic Anderson Model
(拡張周期アンダーソンモデルにおける価数不安定性)
2008年3月 - 勝野 弘康
ヘテロエピタキシャル系における転位と結晶表面形態の研究
2007年3月 - 内藤 聖之
鉄の強磁性相における準粒子状態の研究
2007年3月 - 矢田 圭司
層状コバルト酸化物NaxCoO2の磁気的性質および超伝導発現機構の理論的研究
2007年3月
[master's Theses]
- 安藤 叡史
銅酸化物高温超伝導体における反強d波ボンド秩序下の多体電子状態
2022年3月 - 伊藤 美沙子
鉄カルコゲナイド超伝導体の3次元モデルの作成および電子状態の解析
2022年3月 - 齋藤 正樹
単一成分分子性導体[Ni(hfdt)2] のディラックノーダルラインと金属絶縁体クロスオーバー
2022年3月 - 平田 徹
遷移金属ダイカルコゲナイド(TMD)1T-TaS2における非従来型軌道電荷密度波機構
2022年3月 - 安藤 智大
NaFeAs における強的・反強的秩序下での準粒子干渉の解析
2021年3月 - 今川 拓郎
κ−(BEDT−TTF)2X におけるスピン揺らぎによるボンド秩序と輸送現象の理論
2021年3月 - 川島 惇
グラフェンおよびツイスト2層グラフェンにおける電子状態と超伝導発現機構
2021年3月 - 川村 泰喜
単一成分分子性ディラックノーダルライン系における電子状態およびエッジ誘起スピン密度波
2021年3月 - 谷 雄大
有機ディラック電子系における強磁場下での電子相関効果
2020年3月 - 藤江 和也
高ホールドープ鉄系超伝導体における超伝導状態の理論研究
2020年3月 - 大木 大悟
有機ディラック電子系α-(BEDT-TTF)2I3における非一様電荷秩序と直流・光学伝導率
2019年3月 - 杉原 慶昭
五軌道模型を用いた鉄系超伝導体における準粒子干渉の理論研究
2019年3月 - 松原 舜
強相関電子系のエッジやアンドレーエフ束縛状態がもたらすスピン揺らぎの増大および表面d+ip波超伝導
2019年3月 - 竹内 理紗
Theoretical research on the peak structures observed in inelastic neutron scattering of iron-based superconductors
2018年9月 - 川口 功起
銅酸化物高温超伝導体のおけるスピン揺らぎ誘起多段CDWの理論研究
2018年3月 - 田財 里奈
結合定数バーテックス補正を考慮した超伝導理論-軌道・電荷揺らぎによるトリプレット及びシングレット超伝導-
2017年3月 - 松岡 毅
FeSeにおける動的スピン感受率の理論研究
2017年3月 - 中岡 宏徳
BaTi2As2Oにおけるバーテックス補正を考慮した軌道秩序の研究
2016年3月 - 松岡 勝嗣
LaFeAsO1-xHxの高ドープ領域での構造相転移および電子状態の研究
2016年3月 - 佐 里奈
繰り込み群法を用いた1次元電荷秩序の研究
2015年3月 - 松野 元樹
固体中のディラック電子系における長距離クーロン相互作用の効果
2015年3月 - 大野 祐輔
Ru酸化物のトリプレット超伝導発現機構の理論研究:バーテックス補正の効果
2014年3月 - 西浦 秀和
鉄系超伝導における磁気・超伝導共存相の理論
2014年3月 - 宮原 和之
固体中における質量ゼロのディラック電子系に対する円偏光照射の効果
2014年3月 - 井上 善夫
鉄系超伝導体における不純物誘起軌道秩序の理論的研究
2013年3月 - 江口 貴亮
分子性導体のディラック電子系におけるバレーホール効果と軌道磁化
2013年3月 - 川口 将司
粒子源に導かれる櫛歯状パターンへの異方性およびノイズの効果
2013年3月 - 小谷 明弘
2次元ヘリウム3における動的応答関数の研究
2013年3月 - 小谷 明弘
2次元ヘリウム3における動的応答関数の研究
2013年3月 - 津村 卓弥
傾斜ディラックコーンを持つ二次元電子系におけるクライン・トンネリング
2013年3月 - 西下 宗志
3d遷移金属強磁性体における電子相関効果の研究
2013年3月 - 山下 真吾
多重連結した4He薄膜における超流動の研究
2013年3月 - 齋藤 哲郎
軌道揺らぎ理論による鉄系超伝導体のギャップ関数の解析
2012年3月 - 八木 裕一郎
パイロクロア格子上の古典的Heisenberg模型の研究
2012年3月 - 近藤 信二
移動する粒子源によるステップのパターン形成
2011年3月 - 丁子 丈士
バンド縮退を持つ有機導体におけるベリー曲率
2011年3月 - 長谷川 浩也
第一原理計算に基づく鉄砒素系超伝導体の3次元バンド構造の研究
2011年3月